翻开数学课本时,我们常会看到附录里那几页密密麻麻的数字表格——三角函数表。它就像一本数学词典,记录着角度与三角函数值之间的对应关系。记得高中时我第一次接触三角函数表,那种通过查表就能得到sin30°精确值的新奇感,至今记忆犹新。
三角函数表的定义与组成
三角函数表本质上是个对应关系数据库。它将角度作为输入,输出对应的正弦(sin)、余弦(cos)、正切(tan)等函数值。传统印刷表格通常按角度从小到大排列,每行包含角度值和相应的三角函数值。
表格的精度各不相同。有些只精确到度,有些则精确到分甚至秒。精度越高,表格越庞大,但提供的数值也越精确。早期的航海家和天文学家就是依靠这些表格进行复杂计算的。
常用三角函数表类型介绍
常见的三角函数表主要分为完整表和简化表两类。完整表覆盖0°到90°所有角度,间隔通常为1°或更小。简化表则只列出特殊角度值,比如0°、30°、45°、60°、90°这些关键点。
从呈现方式看,还有直角坐标表和极坐标表的区别。直角坐标表直接给出角度与函数值的对应,极坐标表则更适用于向量和复数运算。不同类型的表格服务于不同的计算需求。
角度制与弧度制的转换关系
角度和弧度是描述角大小的两种单位。就像米和英尺都能测量长度,它们之间存在着确定的换算关系。180°等于π弧度,这个基本关系是两种制度转换的桥梁。
转换其实很简单。角度转弧度用乘以π/180,弧度转角度则乘以180/π。比如90°转换成弧度就是90×π/180=π/2。实际查表时需要注意表格使用的单位,现代表格通常会同时标注两种单位制。
三角函数表的设计确实很人性化,它把复杂的函数计算转化为简单的查找操作。在计算器普及之前,这些表格是工程和科学领域不可或缺的工具。即使现在,理解表格背后的原理对我们掌握三角函数本质仍然很有帮助。
那些密密麻麻的数字表格看起来令人头疼,其实藏着不少记忆的捷径。我记得大学时为了准备期末考试,和室友一起研究出几种特别管用的记忆方法,考试时不用查表就能快速得出答案,那种成就感至今难忘。
特殊角三角函数值记忆技巧
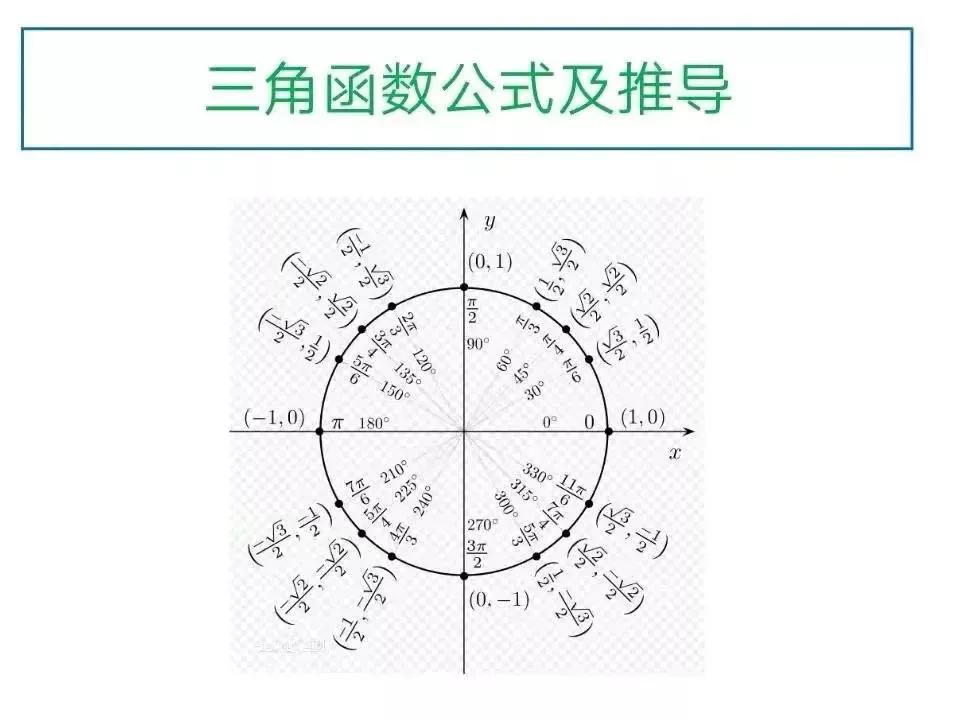
特殊角就像三角函数世界里的地标建筑,记住了它们就掌握了整个坐标系的关键节点。0°、30°、45°、60°、90°这几个特殊角的函数值其实很有规律。
观察sin值从0°到90°的变化:0、1/2、√2/2、√3/2、1。分子部分恰好是√0、√1、√2、√3、√4的开方结果。cos值则完全相反,从1递减到0。这种对称性让记忆变得轻松许多。
正切值的记忆可以借助一个简单规律:tanθ = sinθ/cosθ。特殊角中,tan0°=0,tan45°=1,tan90°不存在,这些边界点很容易记住。30°和60°的正切值互为倒数,这个关系能帮你节省一半的记忆量。
三角函数图像与值域关联记忆
把数字和图形结合起来记忆效果会好很多。想象正弦曲线像起伏的波浪,从原点开始上升,在90°达到顶峰,然后下降。余弦曲线则像波浪的另一个相位,从最高点开始下降。
正弦函数在0°到90°区间内,值域从0增加到1,这个增长过程是平滑的曲线。余弦函数恰好相反,从1减小到0。正切函数在这个区间从0开始快速增长,接近90°时趋向无穷大。
我经常建议学生在纸上随手画出这几个关键点的位置,视觉记忆往往比纯数字记忆更持久。当你看到sin60°,脑海里应该能浮现出那个点在曲线上的位置。
记忆口诀与规律总结
“一二三,三二一,三分之根号不能少”这个口诀帮我记牢了特殊角的三角函数值。具体来说,sin在0°、30°、45°、60°、90°的值可以记为:√0/2、√1/2、√2/2、√3/2、√4/2。
另一个实用的规律是互补角关系:sin(90°-θ)=cosθ,cos(90°-θ)=sinθ。这意味着你只需要记住0°到45°的值,就能推导出45°到90°的所有函数值。
正切和余切也有类似规律:tan(90°-θ)=cotθ。这些对称关系大大减少了需要记忆的内容量。实际上,熟练之后你会发现,真正需要死记硬背的只有四五个关键值,其他都能快速推导出来。
这些记忆方法确实很实用,它们把枯燥的数字变成了有生命力的规律。当我发现不用查表就能心算出三角函数值时,那种数学带来的愉悦感是难以言喻的。
那些看似枯燥的三角函数表,其实在我们生活的各个角落默默发挥着作用。记得有次帮朋友测量老房子翻新的屋顶坡度,靠着三角函数表快速算出了需要的材料长度,那种将书本知识转化为实际解决方案的满足感,至今记忆犹新。
工程测量与建筑领域应用
在建筑工地,三角函数表是工程师的得力助手。测量斜坡角度、计算屋顶坡度、确定支撑结构的最佳角度,这些都需要精确的三角函数值。比如要计算一个坡度为30°的屋顶,施工人员可以直接查表得到sin30°=0.5,cos30°≈0.866,快速算出屋顶的实际高度和水平投影长度。
桥梁建设中,悬索桥的缆索角度计算离不开三角函数。工程师需要根据桥塔高度和主跨距离,精确计算缆索的受力分布。记得参观过一个桥梁施工现场,工程师们手持的函数表已经被翻得卷边,上面密密麻麻标注着各种角度对应的正切值,用于计算不同位置的缆索倾角。
在地理测绘中,测量员利用三角函数计算不可直接测量的距离。通过测量基线和两个角度,就能确定远处目标的位置。这种三角测量法在土地勘测、地图制作中应用广泛,其核心就是三角函数表的准确数值。
物理运动学问题求解
抛体运动分析是三角函数表的经典应用场景。当物体以某个角度抛出时,它的运动轨迹可以分解为水平和垂直两个方向。通过查表获得对应角度的正弦和余弦值,就能快速计算物体的射程、最大高度和飞行时间。
我记得高中物理实验课上,我们用三角函数表计算斜面上小车的加速度。只需要测量斜面角度,查表得到sinθ值,就能根据公式a=gsinθ算出理论加速度值。这个简单的实验让我第一次体会到三角函数在实际问题中的威力。
在圆周运动分析中,三角函数表帮助计算向心加速度的分量。当物体做匀速圆周运动时,其在某个方向上的加速度分量正好与该方向对应的三角函数值成正比。这种关系在机械设计、游乐设施安全分析中都有重要应用。
电子技术与信号处理应用
交流电路分析深深依赖三角函数表。在计算阻抗、相位差、功率因数时,工程师需要频繁查询不同角度对应的三角函数值。比如在RLC串联电路中,总阻抗的相位角就需要通过arctan函数来确定,这个值直接影响电路的性能。
信号处理领域,三角函数表是理解傅里叶变换的基础。任何复杂信号都可以分解为不同频率的正弦波组合,而每个频率成分的幅度和相位都需要用到三角函数计算。在数字滤波器设计中,特定频率的响应计算也离不开准确的函数值查询。
无线通信中的调制解调过程,三角函数表扮演着关键角色。调相和调频技术本质上都是对载波信号的相位或频率进行三角函数运算。虽然现代设备都用数字计算,但基本原理仍然建立在那些经典的函数关系之上。
这些应用场景让我深刻感受到,三角函数表不仅是数学工具,更是连接理论与实践的桥梁。当看到自己计算的函数值帮助解决了实际问题时,那种成就感确实很特别。
翻开泛黄的三角函数表,那些密密麻麻的数字曾经让很多初学者望而生畏。但掌握正确的查表方法后,你会发现这张表就像一位忠实的朋友,总能在需要时给出准确的答案。我至今保留着大学时用的那本函数手册,书页边缘还留着当时用铅笔做的各种标记,记录着不同场景下的查表心得。
精确查表与近似取值方法
查表时最让人困扰的可能是遇到表上没有的中间值。比如要找sin47.5°,而表上只有sin47°和sin48°的值。这时候可以采用线性插值法:先记录sin47°≈0.7314,sin48°≈0.7431,两者的差值是0.0117。因为47.5°正好在中间位置,所以sin47.5°≈0.7314 + 0.0117/2 = 0.7373。这种方法在工程计算中足够精确。
实际应用中并不总是需要极高的精度。在快速估算时,可以记住几个关键角度对应的函数值。sin30°=0.5,sin45°≈0.707,sin60°≈0.866,这些特殊角度的数值能帮你快速验证查表结果的合理性。记得有次在施工现场,工程师直接用心算的近似值指导工人调整支撑架角度,误差完全在允许范围内。
查表时要注意角度的单位一致性。有些表格使用度分秒格式,比如35°15',这时候需要先将分秒转换为十进制度数。35°15'就等于35 + 15/60 = 35.25°。这个转换步骤虽然简单,却经常被忽略而导致错误。
反三角函数查表技巧
反三角函数的查表需要一些逆向思维。当已知函数值求角度时,比如知道sinθ=0.6428,要在表中找到最接近这个值的正弦数,然后对应回角度。这个过程就像在玩数字侦探游戏,需要细心比对。
表格中通常不会列出所有可能的函数值,这时候需要反向插值。假设表中sin31°=0.5150,sin32°=0.5299,而我们需要求arcsin0.5220对应的角度。计算差值比例(0.5220-0.5150)/(0.5299-0.5150)≈0.47,所以角度≈31°+0.47°≈31.47°。这个方法在工程计算中特别实用。
反余弦和反正切的查表原理相同,但要注意它们的值域范围。反余弦的值域是[0,π],而反正切的值域是(-π/2,π/2)。这些特性会影响最终结果的选取,特别是在解三角形问题时尤为重要。
查表误差分析与修正
任何查表过程都存在误差,了解这些误差的来源很重要。制表时的四舍五入会产生截断误差,通常三角函数表的精度在0.0001左右。插值计算会引入方法误差,线性插值假设函数变化是线性的,但实际上三角函数的变化并非完全线性。
误差会随着计算步骤累积。比如先用插值法查sin值,再用这个值求arcsin,误差可能被放大。在要求精密的计算中,这种累积误差需要考虑。我遇到过的一个案例是,天文观测中的角度计算因为多次查表插值,最终结果偏差了0.1°,虽然看起来很小,但在天文尺度上这个误差已经相当可观。
修正误差的一个实用技巧是交叉验证。用不同的三角函数关系来验证结果的合理性。比如已知sinθ,可以计算cosθ=√(1-sin²θ),然后查表验证这个cos值对应的角度是否一致。这种多重验证能有效发现并纠正查表错误。
查表不只是机械地查找数字,更是一种需要理解和技巧的过程。每次准确找到需要的数值时,那种解决问题的成就感确实让人着迷。现在的计算工具越来越先进,但理解这些基础查表方法,能让你在关键时刻多一份把握。
那些厚重的三角函数手册现在更多是收藏品了。翻开它们会闻到旧纸张特有的味道,让我想起大学图书馆里整排的数学参考书。但三角函数表并没有消失,它们以全新的形式融入我们的数字生活。上周帮侄子做物理作业时,他直接用手机计算器查三角函数值,那种便捷让我不禁感叹技术的进步。
计算机编程中的三角函数实现
编程语言处理三角函数的方式很巧妙。它们不再依赖预计算的表格,而是使用数学库中的近似算法。比如C语言的math.h库提供sin()、cos()、tan()等函数,这些函数内部使用多项式逼近或CORDIC算法来计算任意角度的三角函数值。
Python的math模块让三角函数计算变得异常简单。只需要import math,然后调用math.sin(math.pi/6)就能得到0.5。这种抽象层次让开发者无需关心具体实现细节。记得第一次用Python写物理仿真程序时,这种便利性让我节省了大量时间。
游戏开发中三角函数的应用更加频繁。角色移动轨迹、摄像机角度旋转、物理引擎的碰撞检测,到处都需要实时计算三角函数。现代游戏引擎会针对性能进行优化,甚至使用查找表结合插值的方法来平衡精度和速度。Unity引擎中的Mathf类就提供了大量优化过的三角函数方法。
智能手机计算器的三角函数功能
手机计算器应用可能是普通人接触三角函数最直接的途径。从简单的基础计算模式切换到科学计算器,立即就能看到sin、cos、tan等按钮。这些应用通常支持角度制和弧度制的切换,满足不同场景的需求。
实际使用中会发现一些贴心的设计细节。比如输入sin(90)后立即显示结果1,而不需要输入度符号。这种智能识别大大提升了用户体验。有些计算器应用还提供历史记录功能,可以回溯之前的计算步骤,特别适合学生验证作业答案。
我注意到不同厂商的计算器应用在处理精度上有所差异。测试了几款主流手机的计算器,发现它们显示的有效数字位数不同,但核心计算结果基本一致。这种标准化确保了无论使用什么设备,都能获得可靠的三角函数值。
在线三角函数表工具推荐
网络上有大量优质的三角函数资源。Desmos和GeoGebra这类在线图形计算器不仅能提供函数值,还能实时显示函数图像变化。这种可视化方式极大帮助了理解三角函数的概念本质。
Wolfram Alpha作为计算知识引擎,在三角函数计算方面表现出色。它不仅能给出精确值,还提供连分数展开、级数表示等高级数学信息。对于需要深入理解三角函数性质的学习者来说,这是不可多得的工具。
专门的教学网站如Khan Academy和Brilliant.org提供了交互式三角函数学习模块。这些平台将传统三角函数表的概念与现代教学理念结合,通过渐进式练习帮助用户掌握核心知识。它们的移动端应用让学习可以随时随地进行。
技术改变了我们使用三角函数表的方式,但数学的本质从未改变。从纸质表格到智能算法,变的只是工具,不变的是对精确计算的追求。每次点击手机计算器上的sin按钮时,我都会想起那些在图书馆查表的日子,这种跨越时代的连接确实很奇妙。